`a' = 8*Rsin(A/3)sin(B/3)sin(C/3)`

Enter a value for all fields

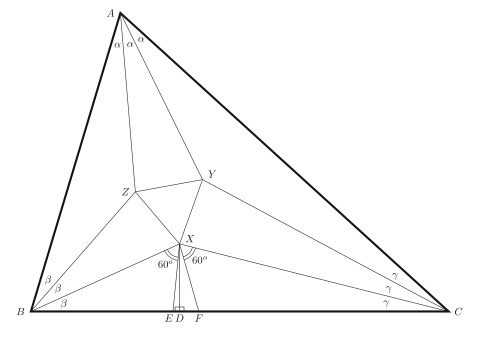
Elementary proof of Morley's trisector theorem.

Morley's Trisector Theorem states that in any triangle, the three points of intersection of the adjacent angle trisectors form an equilateral triangle, called the first Morley triangle or simply the Morley triangle. It has various generalizations; in particular, if all of the trisectors are intersected, one obtains four other equilateral triangles.
The following formula is used to find the side lengths: `a'=8Rsin(A/3)sin(B/3)sin(C/3)`, where: 

• `R` = circumradius
• `A` = angle A in original triangle
• `B` = angle B in original triangle
• `C` = angle C in original triangle

References

Wikipedia (https://en.wikipedia.org/wiki/Morley%27s_trisector_theorem)